Matlab: Messwertfilter

Messwertfilter:

Verfahren:

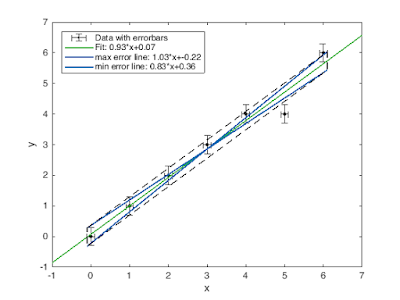
(English) Die Matlab-Funktion ist dazu da, Messwerte mit großen Abweichungen bei linearen Zusammenhängen zu filtern und durch die restlichen Messwerte die Funktion zu fitten. Ansich funktioniert diese Funktion ähnlich wie die Fehlergeradenfunktion, bei der eine Gerade durch die y-Werte mit deren maximalen Fehler und eine Gerade durch die y-Werte mit deren minimale Fehler gefittet wird. Dabei kann in der Funktion entschieden werden, wie große Abweichungen zugelassen werden, sprich welche prozentuale Abweichung zu den Fehlerwerten.
Wenn ein Wert gefiltert wird, wiederholt sich die Filterfunktion und überprüft mit dem neuen fit, ob wieder Messwerte außerhalb dem Fehlerbereich sind. Folgende Abbildung veranschaulicht die Funktionsweise:

 

Hierbei ist in rot die Fehlerbox und der gefilterte Messwert.

 Implementieren:

Die Funktion kann die Fehlerbox und die gefilterten wie auch nicht gefilterten Werte zurückgeben und wird wie folgt in Matlab aufgerufen:"[x,y,xerr,yerr,xaus,yaus,xerraus,yerraus] = filterfunc(x, y, xerr, yerr, scale, count)". Dabei sind "xaus,yaus" die gefilterten x- und y-Werte und "xerraus,yerraus" die gefilterten x- und y-Fehlerwerte.
Die Filterfunktion hat sechs Argumente, wobei "x,y,xerr,yerr" die Werte mit ihren Fehlern sind. Falls kein x-Fehlerwert existiert kann einfach "0" eingegeben werden. "Scale" gibt an wie stark gefiltert werden soll. Für (scale = 1) wird genau die Abweichung der eingegeben y-Fehler verwendet. Für kleinere Faktoren wird folglich die Box kleiner und somit mehr Messwerte gefiltert.
Wie folgt sind vier plots mit verschiedenen scale-Faktoren zu sehen:

Mit dem letzten Argument (count), wird für (count = 1) die Fehlerbox geplottet, für alle anderen Werte wird nichts geplottet sondern nur die Rückgabewerte geben.

Quellcode:

function [x,y,xerr,yerr,xaus,yaus,xerraus,yerraus] = filterfunc(x, y, xerr, yerr, scale, count)
%This function filters the values, which are imprecise. 'Scale' is a
%parameter for this imprecise. With 'scale=1' the imprecise is exacly your
%y-error. With count '1' this function plots the errorbox'.
%If the measured point is outside the area, this function will
%take the values out and give it back at 'xaus, yaus, xerraus, yerraus'.


l=numel(x);
if(xerr==0)
    xerr=zeros([l,1]);
endymax=y+scale*yerr
ymin=y-scale*yerr
fitmax=fit(x,ymax,@(a,b,x) a*x+b);
fitmin=fit(x,ymin,@(a,b,x) a*x+b);
fitVal=fit(x,y,@(a,b,x) a*x+b);

%Fit the maximal and the minimal errorlines through the mesured values with
%their deviations.
a=coeffvalues(fitmax);
b=coeffvalues(fitmin);

amax=a(1);
amin=b(1);
bmax=a(2);
bmin=b(2);

xaus=[];
yaus=[];
xerraus=[];
yerraus=[];

yp=x*amax+bmax;
ym=x*amin+bmin;
n=1;
%filter the values with a large imprecision
while(1==1)
    altamax=amax;
    altbmax=bmax;
    altamin=amin;
    altbmin=bmin;
    for i=1:1:l
        if (i>l)
            break;
        end
        if( (y(i)>(yp(i)+yerr(i)*(scale-1))) | (y(i)<(ym(i)-yerr(i)*(scale-1))) )
            xaus(n)=x(i);
            yaus(n)=y(i);
            xerraus(n)=xerr(i);
            yerraus(n)=yerr(i);
            x(i)=[];
            y(i)=[];
            yp(i)=[];
            ym(i)=[];
            xerr(i)=[];
            yerr(i)=[];
            i=i-1;
            l=l-1;
            n=n+1;
        end
    end
    if (numel(x)>1)
        fitmax=fit(x,y+yerr*scale,@(a,b,x) a*x+b);
        fitmin=fit(x,y-yerr*scale,@(a,b,x) a*x+b);
    end
    a=coeffvalues(fitmax);
    b=coeffvalues(fitmin);
    amax=a(1);
    amin=b(1);
    bmax=a(2);
    bmin=b(2);
    %if in this cycle the fits are equal, then close the function 
    if (abs(altamax-amax)<1e-6 & abs(altbmax-bmax)<1e-6 & abs(altamin-amin)<1e-6 & abs(altbmin-bmin)<1e-6)
        break;
    end
            
end
if (n==1)
    xaus=[];
    yaus=[];
    xerraus=[];
    yerraus=[];
end
l=numel(x)
if (l>=2)
    l=numel(x);

    %Declare the 4 corners of the box
    xlu=x(1)-xerr(1);
    xld=x(1)-xerr(1);
    xru=x(l)+xerr(1);
    xrd=x(l)+xerr(1);

ylu=amax*xlu+bmax;
yru=amax*xru+bmax;
yld=amin*xld+bmin;
yrd=amin*xrd+bmin;

%Declare the vectors of the corners.
xcorner=[xlu xru xrd xld xlu];
ycorner=[ylu yru yrd yld ylu];

if (count == 1)
    hold on;
    plot(xcorner,ycorner,'--','Color',[0.8 0 0.2]);
end
end

if (l==0)
    display('All measurpoint are acapetable');
end
if (numel(x)==0)
    display('No points are in that scale');
end
end