Matlab: Dijkstra Methode - kürzestes Weg entlang des Gradienten (kleine Nachbarschaft)

Die Dijkstra Methode

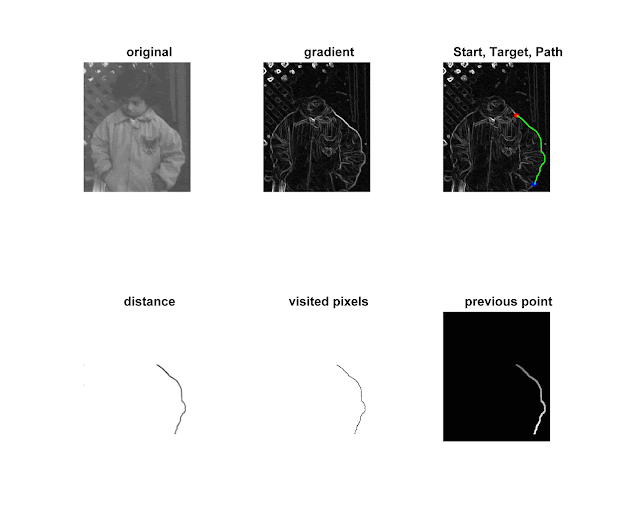
(English) In diesem Post zeige ich wie mit Matlab am Rand von Objekten oder Bildern der Pfad gefunden werden kann. Hierfür benutzt ich die Dijkstra Methode. Ich nehme als Input ein BIld von Matlab, führe es in ein Gradientenbild über mit [G,Gdir] = imgradient(img,'sobel'); und benutze meine Funktion Dijkstra(G,p,q):
Diese ist benötigt ein Bild in double Format G, einen Startpunkt p bei dem der erste Wert der Zeilenwert und der zweite der Spaltenwert ist und das vorgegebene Ziel q dem entsprechend.
Die Methode funktioniert so, dass sie alle Distanzen auf unendlich setzt und nur den Startpunkt auf 0. Alle unbesichteten Pixel haben den Wert 1. Der Algorithmus geht so lange, bis das Ziel kein unbesichteter Pixel mehr ist. Er summiert über alle Nachbarpixel und berechnet immer das Gewicht bzw. die Distanz mit function [weight] = localedgewidth(G,p,q) wobei der Wert vom Nachbarpixel von dem Maximum der Bilder abgezogen wird, dies durch die Differenz von maximalen und minimalen Wert des Bildes geteilt und mit der Distanz multipliziert. Ist das Gewicht kleiner dem Abstand wird die Distanz überschrieben und der vorherige besuchte Pixel gespeichert. Sobald der aktuelle Wert kleiner dem Wert davor ist, wird beim nächsten Pixel das Selbe wiederholt.
Um den Pfad zu rekonstruieren wird solange der Pfad mit Null gleich gesetzt bis man wieder am Startpunkt ist.
Dann kann die Distanz, der Pfad, die unbesichteten Pixel und die vorher besichteten Pixel ausgegeben werden.
Hier ein kleines Beispiel, welches weiter unten im Quellcode aufgeführt ist.

Hier kann der Code bei MathWorks heruntergeladen werden.

Quellcode Dijkstra:

function [path, prev, unvis, distance] = Dijkstra(Matrix, start, target)
%Matrix is the incoming image
%start is the start point in a vector [a,b] where a is the column and b the
%row
%target is the end point similare to start
%path is the matrix with ones excepted at the position of the path where it is 0
%prev are also the previous visited pixels where the algorithm took the
%wrong way
%unvis are all unvisited pixels
%distance is the distance or weight of the pixels

%calculate amount of nodes
    n = size(Matrix);

    unvis = ones(n); %set all unvisited to 1
    distance = ones(n).*inf; %set all distances to inf
    prev = zeros(n);%previous node

    u = start;
    distance(start) = 0;%start distance is 0

    while (unvis(target(1),target(2))==1)
        test = inf;
        for i=1:1:3%sum over the neighborhood pixels
            for j=1:1:3
                if(i~=2 | j ~=2)%exclude the pixel u in the middle
                    vx = u(1)-2+i;%generate the neighborhood pixels (3x3)
                    vy = u(2)-2+j;
                    v = [vx vy];
                    if (unvis(vx,vy)==1)%if actual neighbor is unvisited
                        cost = localedgewidth(Matrix,u,v);%calculate the weight
                        if (cost<distance(vx,vy))
                            distance(vx,vy)=cost;
                            prev(vx,vy)=u(1)*n(2)+u(2);%set previous node
                            if (cost<test)
                                next=[vx vy]; 
                                test=cost;
                            end
                        end
                    end
                end
            end
        end 
        unvis(u(1),u(2))=0;
        u=next;
    end
    path=ones(n);
    u = target;
    %backtrack from end to start to find best sequence
    while u ~= start
        previous=prev(u(1),u(2));
        k=floor(previous/n(2));
        l=previous-k*n(2);
        path(k,l)=0;%generate path
        u=[k,l];
    end

end

function [weight] = localedgewidth(G,p,q)
% aclculate the local edge width between neighborhood pixels
    maxG=max(G(:));
    minG=min(G(:));
    d=sqrt(sum((p-q).^2));
    weight=(maxG-G(q(1),q(2)))/(maxG-minG)*d/sqrt(2);
end

 

Quellcode Anwendung:

 clear;
clc;

img = imread('pout.tif');
img = im2double(img);
%a)
[G,Gdir] = imgradient(img,'sobel');
n = size(G);
p = [120 165];
q = [274 205];

[path, prev, unvis, distance] = Dijkstra(G, p, q);
% use my function and plot everything
fig(1) = figure(1);
clf(1);
subplot(2,3,1);hold on;imshow(img);title('original');
subplot(2,3,2);hold on;imshow(G);title('gradient');
subplot(2,3,3);hold on;imshow(G);plot(165,120,'r.','markersize',12);
plot(205,274,'b.','markersize',12);title('Start, Target, Path');
for i=1:1:n(1)
    for j=1:1:n(2)
        if path(i,j) == 0
            plot(j,i,'g.','markersize',1);
        end
    end
end
subplot(2,3,4);hold on;imshow(distance);title('distance');
subplot(2,3,5);hold on;imshow(unvis);title('visited pixels');
subplot(2,3,6);hold on;imshow(mat2gray(prev));title('previous point')